Ис­сле­до­ва­ние устой­чи­во­сти хода при­цеп­ной жатки.

Автор: Ми­шу­ст­ин В.В., кан­ди­дат тех­ни­че­ских наук.

Ис­то­рия во­про­са.

Из­вест­ные ме­то­ды рас­че­та устой­чи­во­сти хода при­цеп­ной жатки по сути сво­ди­лись к опре­де­ле­нию за­па­са по сцеп­ле­нию колес с грун­том при бо­ко­вом сдви­ге и на­хож­де­нию на ос­но­ва­нии этого необ­хо­ди­мой длины сницы. Во вни­ма­ние при­ни­ма­лись толь­ко пре­дель­ные зна­че­ния ха­рак­те­ри­стик грун­та, так на­зы­ва­е­мый ко­эф­фи­ци­ент со­про­тив­ле­ния бо­ко­во­му сдви­гу φсц.

Таким об­ра­зом, пол­но­стью не рас­смат­ри­ва­лись про­цес­сы, свя­зан­ные с де­фор­ма­ци­ей грун­та и упру­ги­ми свой­ства­ми пнев­ма­ти­че­ских шин. Од­на­ко, как по­ка­зы­ва­ет опыт, дви­же­ние при­цеп­ной жатки даже в бла­го­при­ят­ных усло­ви­ях по сцеп­ле­нию колес с грун­том про­ис­хо­дит под неко­то­рым углом и с от­ста­ва­ни­ем по­ле­во­го де­ли­те­ля.

Дви­же­ние жатки с от­кло­не­ни­ем ее про­доль­ной оси от на­прав­ле­ния дви­же­ния свя­за­но с уво­дом колес, обу­слов­лен­ным де­фор­ма­ци­ей грун­та и эла­стич­но­стью пнев­ма­ти­че­ской шины.

Эти про­цес­сы давно по­па­ли в поле зре­ния ав­то­мо­би­ли­стов, а затем и са­мо­ле­то­стро­и­те­лей. Впер­вые увод колес рас­смат­ри­вал М.Г. Бек­кер, затем ака­де­мик Е.А. Чу­да­ков и при­ме­ни­тель­но к са­мо­ле­ту ака­де­мик М.В. Кел­дыш. Эти ра­бо­ты до сих пор яв­ля­ют­ся ос­но­во­по­ла­га­ю­щи­ми при рас­смот­ре­нии дви­же­ния эла­стич­но­го ко­ле­са по твер­до­му по­кры­тию. При­ме­ни­тель­но к рас­смат­ри­ва­е­мо­му во­про­су, необ­хо­ди­мо учи­ты­вать еще де­фор­ма­цию грун­та.

Ис­ле­до­ва­ние.

При мед­лен­ном рав­но­мер­ном дви­же­нии жатки, когда силы инер­ции можно не учи­ты­вать, схема сил, на­прав­ле­ния ско­ро­стей и углы увода δув с уче­том со­став­ля­ю­щих де­фор­ма­ций пнев­ма­ти­че­ских шин и грун­та по­ка­за­ны на ри­сун­ке 1. При этом для обес­пе­че­ния сов­ме­ще­ния на­прав­ле­ния про­доль­ной оси жатки с на­прав­ле­ни­ем дви­же­ния осу­ществ­ле­на уста­нов­ка колес под неко­то­рым углом Θ рав­ным углу увода колес δув.
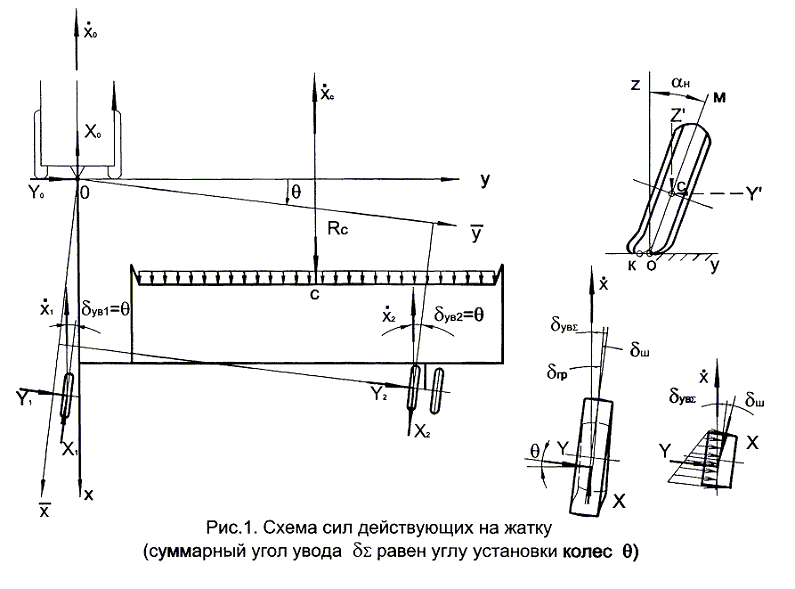
Рисунок 1. Схема сил действующих на жатку.

Важно, что бо­ко­вые ре­ак­ции на ко­ле­са со сто­ро­ны грун­та все­гда на­прав­ле­ны пер­пен­ди­ку­ляр­но плос­ко­сти ко­ле­са. От­кло­не­ние ре­ак­ций может быть обу­слов­ле­но толь­ко тре­ни­ем в под­шип­ни­ках, ко­то­рым в дан­ном слу­чае можно пре­не­бречь.

При этих усло­ви­ях урав­не­ния рав­но­ве­сия жатки будут иметь вид:

  • ∑Mo = Y1 * x1 - X1 * y1 + Y2 * x2 - X2 * y2 + Rc * yc = 0
  • ∑Xi = X1 * cos(Θ) + Y1 * sin(Θ) + X2 * cos(Θ) + Y2 * cos(Θ) + Rc Xo = 0    (1)
  • ∑Yi = Y1 * cos(Θ) - X1 * sin(Θ) + Y2 * cos(Θ) - X2 * sin(Θ) - Yo = 0

где

  • Rc — рав­но­дей­ству­ю­щая сил со­про­тив­ле­ния ножа и мо­то­ви­ла
  • X1, X2 — силы со­про­тив­ле­ния пе­ре­ка­ты­ва­нию колес
  • Y1, Y2 — силы со­про­тив­ле­ния бо­ко­во­му сдви­гу колес
  • x1, y1, x2, y2 — плечи дей­ствия рав­но­дей­ству­ю­щих сил, по­лу­чен­ные с по­мо­щью пре­об­ра­зо­ва­ния де­кар­то­вых пря­мо­уголь­ных ко­ор­ди­нат при по­во­ро­те осей на угол Θ:
    • x = x * cos(Θ) + y * sin(Θ)
    • y = -x * sin(Θ) + y * cos(Θ)

При этом по­ло­жи­тель­ным счи­та­ет­ся по­во­рот осей про­тив ча­со­вой стрел­ки, по­сколь­ку в дан­ном слу­чае оси по­во­ра­чи­ва­ют­ся по ча­со­вой стрел­ке, то угол Θ сле­ду­ет под­став­лять со зна­ком минус.

Силы X1  и Х2  опре­де­ля­ют­ся через ко­эф­фи­ци­ен­ты со­про­тив­ле­ния пе­ре­ка­ты­ва­нию колес φx  и из­вест­ные вер­ти­каль­ные ре­ак­ции на ко­ле­са:

  • X1 = φx * Z1
  • X2 = φx * Z2

Бо­ко­вые ре­ак­ции яв­ля­ют­ся функ­ци­я­ми углов увода колес:

  • Y1 = φy(δув)Z1
  • Y2 = φy(δув)Z2

Клю­чом к ре­ше­нию по­став­лен­ной за­да­чи яв­ля­ет­ся за­ви­си­мость ко­эф­фи­ци­ен­та со­про­тив­ле­ния бо­ко­во­му сдви­гу от угла увода колес φy = f(δув), при­ве­ден­ная на ри­сун­ке 2.
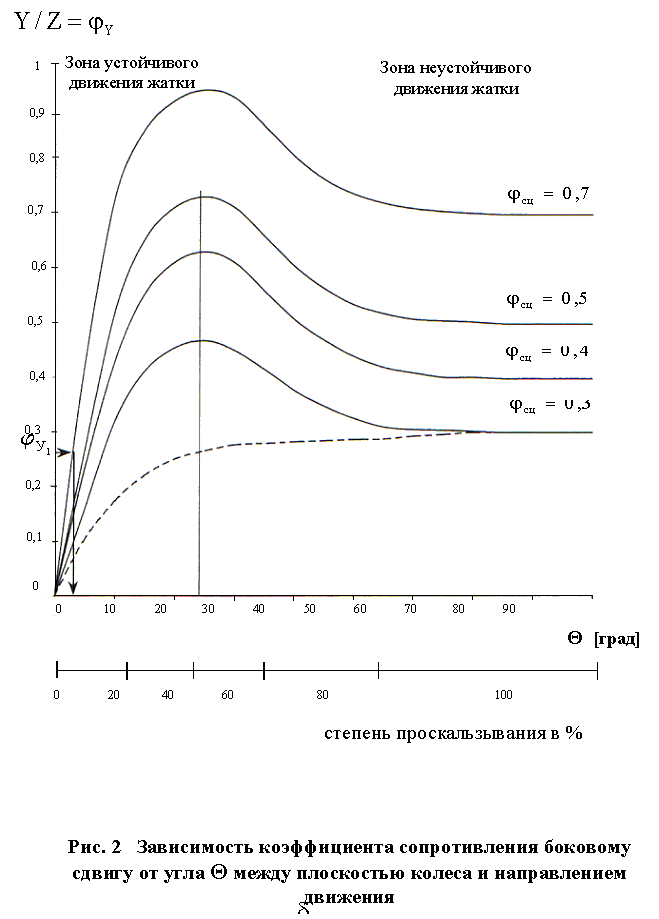
Рисунок 2. График зависимости коэффициента сопротивления боковому сдвигу от угла между плоскостью колеса и направлением движения.

Пред­став­лен­ная за­ви­си­мость от­ра­жа­ет ос­нов­ные фи­зи­че­ские про­цес­сы про­ис­хо­дя­щие при де­фор­ма­ции шины и грун­та. При малых углах увода эта за­ви­си­мость ли­ней­ная и скла­ды­ва­ет­ся из упру­гой де­фор­ма­ции шины и де­фор­ма­ции грун­та. По мере уве­ли­че­ния рас­пре­де­лен­ной бо­ко­вой ре­ак­ции про­ис­хо­дит раз­ру­ше­ние грун­та по всей длине кон­так­та шины с грун­том, при этом де­фор­ма­ция шины до­сти­га­ет мак­си­маль­ной ве­ли­чи­ны, что со­от­вет­ству­ет мак­си­му­му на гра­фи­ке. После этого ко­эф­фи­ци­ент со­про­тив­ле­ния бо­ко­во­му сдви­гу φy  умень­ша­ет­ся. При пол­ном сколь­же­нии шины в бо­ко­вом на­прав­ле­нии ко­эф­фи­ци­ент φy  равен ко­эф­фи­ци­ен­ту тре­ния сколь­же­ния φсц  и это чис­лен­ное зна­че­ние обыч­но и при­во­дит­ся в ли­те­ра­тур­ных ис­точ­ни­ках в ка­че­стве ко­эф­фи­ци­ен­та со­про­тив­ле­ния бо­ко­во­му сдви­гу. Такая за­ви­си­мость ха­рак­тер­на для связ­ных грун­тов, для несвяз­ных (сы­пу­чих) грун­тов кри­вая носит дру­гой ха­рак­тер и не имеет мак­си­му­ма.

Пред­став­лен­ные на ри­сун­ке 2 за­ви­си­мо­сти поз­во­ля­ют опре­де­лить необ­хо­ди­мый угол уста­нов­ки колес Θ. По­сколь­ку бо­ко­вые ре­ак­ции Y1  и Y2  яв­ля­ют­ся функ­ци­я­ми углов увода колес, то урав­не­ние рав­но­ве­сия (1) яв­ля­ют­ся транс­це­дент­ным и его ре­ше­ния проще всего на­хо­дить ме­то­дом по­сле­до­ва­тель­ных при­бли­же­ний. За пер­вое при­бли­же­ние при­ни­ма­ет­ся ре­ше­ние при Θ = 0.

Рас­чет, вы­пол­нен­ный для при­цеп­ной жатки ЖВ-7, по­ка­зы­ва­ет, что уже тре­тье при­бли­же­ние дает до­ста­точ­ную точ­ность, так как раз­ни­ца между вто­рым и тре­тьим при­бли­же­ни­ем со­став­ля­ет де­ся­тые доли гра­ду­са (смот­ри­те ри­су­нок 2).

Так как в усло­ви­ях при­цеп­ной жатки на ко­ле­са по­сто­ян­но дей­ству­ет бо­ко­вая сила од­но­го на­прав­ле­ния, то необ­хо­ди­мо осу­ще­ствить на­клон колес нав­стре­чу этой силе для умень­ше­ния угла увода колес. Здесь на­ме­рен­но не ис­поль­зу­ет­ся тер­мин «раз­вал колес», также как и рань­ше не ис­поль­зо­вал­ся тер­мин «схо­ди­мость колес», по­сколь­ку на­клон колес осу­ществ­ля­ет­ся в одну сто­ро­ну.

При дей­ствии бо­ко­вой силы в сто­ро­ну про­ти­во­по­лож­ную на­кло­ну ко­ле­са про­ис­хо­дит вы­рав­ни­ва­ние шины и кон­такт шины с грун­том осу­ществ­ля­ет­ся сред­ней ча­стью про­тек­то­ра, что при­во­дит с одной сто­ро­ны к умень­ше­нию из­но­са шины, а с дру­гой к улуч­ше­нию сцеп­ных свойств шины с грун­том. Кроме того рав­но­мер­нее на­гру­жа­ют­ся под­шип­ни­ки оси ко­ле­са.

На­клон колес опре­де­ля­ет­ся по зна­че­нию ко­эф­фи­ци­ен­та со­про­тив­ле­ния уводу от на­кло­на колес Kн = αк / δув, рав­но­му для гру­зо­вых шин 4—6. Это озна­ча­ет, что при на­клоне ко­ле­са на один гра­дус, воз­ни­ка­ет увод, угол ко­то­ро­го равен 10—15 ми­ну­там. Рас­че­ты, вы­пол­нен­ные для при­цеп­ной жатки ЖВ-7 (масса 2160 кг, длина сницы L = 4,057 м, ко­эф­фи­ци­ент со­про­тив­ле­ния пе­ре­ка­ты­ва­нию φx = 0,1, сила со­про­тив­ле­ния от ножей и мо­то­ви­ла Rc = 1750 Н) по­ка­зы­ва­ют, что для фона сухой стер­ни со зна­че­ни­ем ко­эф­фи­ци­ен­та бо­ко­во­му сдви­гу при пол­ном сколь­же­нии φсц = 0,7 ко­ле­са долж­ны быть от­кло­не­ны от про­доль­ной оси на два гра­ду­са впра­во (Θ = 2°) и на­кло­не­ны от вер­ти­ка­ли на че­ты­ре гра­ду­са также впра­во (αк = 4°).

Рас­чет­ные углы уста­нов­ки колес для дру­гих фонов с более сла­бы­ми грун­та­ми (φсц = 0,5…0,3) будут боль­ше, од­на­ко сле­ду­ет при­ни­мать ми­ни­маль­ные углы. В этом слу­чае на фонах с более сла­бы­ми грун­та­ми жатка будет дви­гать­ся с от­кло­не­ни­я­ми про­доль­ной оси впра­во на 1…2 гра­ду­са, то есть будет «от­ста­вать». Од­на­ко, это от­кло­не­ние будет мень­ше, чем при ну­ле­вой уста­нов­ки колес (Θ = 0, αк = 0) как это при­ня­то в су­ще­ству­ю­щих кон­струк­ци­ях.

За­клю­че­ние.

Пред­ло­жен­ный метод поз­во­ля­ет рас­смат­ри­вать устой­чи­вость хода жатки в рам­ках об­ще­при­ня­тых по­ня­тий устой­чи­во­сти дви­же­ния. На участ­ке воз­рас­та­ния ко­эф­фи­ци­ен­та бо­ко­во­го сдви­га слу­чай­ное уве­ли­че­ние сил со­про­тив­ле­ния (вы­зван­ное, на­при­мер, на­ез­дом на пре­пят­ствие пра­вым ко­ле­сом) при­во­дит к воз­рас­та­нию вос­ста­нав­ли­ва­ю­ще­го мо­мен­та, и жатка воз­вра­тит­ся в ис­ход­ное по­ло­же­ние. Если же уве­ли­че­ние сил со­про­тив­ле­ния будет таким, что ре­а­ли­зу­е­мый ко­эф­фи­ци­ент со­про­тив­ле­ния бо­ко­во­му сдви­гу пе­рей­дет через мак­си­мум, то вы­рав­ни­ва­ние жатки будет невоз­мож­но. В этом слу­чае вос­ста­нов­ле­ние хода жатки будет воз­мож­но толь­ко при умень­ше­нии сил со­про­тив­ле­ния, при ко­то­ром ре­а­ли­зу­е­мый ко­эф­фи­ци­ент со­про­тив­ле­ния бо­ко­во­му сдви­гу будет ниже его пре­дель­но­го зна­че­ния φсц.

Вы­пол­нен­ные ис­сле­до­ва­ния поз­во­ля­ют сде­лать сле­ду­ю­щие вы­во­ды. Дви­же­ние при­цеп­ной жатки про­ис­хо­дит с уво­дом колес, обу­слов­лен­ным де­фор­ма­ци­ей пнев­ма­ти­че­ских шин и грун­та. Рас­че­ты, про­ве­ден­ные с уче­том этих фак­то­ров, поз­во­ля­ют опре­де­лить длину сницы и углы уста­нов­ки колес, при ко­то­рых обес­пе­чи­ва­ет­ся устой­чи­вое дви­же­ние жатки без от­кло­не­ния ее про­доль­ной оси от на­прав­ле­ния дви­же­ния. При этом улуч­ша­ют­ся усло­вия ра­бо­ты ре­жу­ще­го ап­па­ра­та, мо­то­ви­ла и по­ле­во­го де­ли­те­ля. Улуч­ша­ют­ся сцеп­ные свой­ства шин с грун­том и рав­но­мер­нее на­гру­жа­ют­ся под­шип­ни­ки осей колес.

Ли­те­ра­ту­ра.

  1. Агей­кин Я.С. Про­хо­ди­мость ав­то­мо­би­лей. —М.: Ма­ши­но­стро­е­ние, 1981. -232 с., ил.
  2. Бек­кер М.Г. Вве­де­ние в тео­рию си­стем мест­ность — ма­ши­на. —М.: Ма­ши­но­стро­е­ние, 1973. -520 с., ил.
  3. Зе­ме­лев Г.В. Тео­рия ав­то­мо­би­ля. —М.: Ма­ш­гиз, 1959. -312 с., ил.
  4. Ила­ри­о­нов В.А. Экс­плу­а­та­ци­он­ные свой­ства ав­то­мо­би­ля. —М.: Ма­ни­но­стро­е­ние, 1966. -280 с., ил.
  5. Кно­роз В.И. под ред., Ра­бо­та ав­то­мо­биль­ной шины. —М.: Транс­порт, 1976. -238 с., ил.
  6. Ми­ро­нен­ко Ю.А. О дви­же­нии од­но­ос­но­го при­це­па. Меж­ву­зов­ский сбор­ник. —Ро­стов-на-До­ну, 1982. с. 129-134, ил.
  7. Чу­да­ков Е.А. Из­бран­ные труды. Т.1. Тео­рия ав­то­мо­би­ля. —Изд-во АН СССР, 1961, -458 с., ил.

Об ав­то­ре.

Ми­шу­ст­ин Ва­ле­рий Ва­си­лье­вич. За­кон­чил МВТУ им. Ба­у­ма­на (ныне МГТУ им. Ба­у­ма­на), Кон­струк­тор­ско-ме­ха­ни­че­ский фа­куль­тет. Ру­ко­во­ди­те­лем ди­плом­но­го про­ек­та был быв­ший глав­ный кон­струк­тор ГАЗа, со­зда­тель пер­во­го по­сле­во­ен­но­го ав­то­мо­би­ля «По­бе­да» А.А. Ли­п­гарт.
Кан­ди­дат тех­ни­че­ских наук. Имеет свыше 30 изоб­ре­те­ний и на­уч­ных пуб­ли­ка­ций. Ра­бо­тал с вы­да­ю­щи­ми­ся спе­ци­а­ли­ста­ми в об­ла­сти спе­ци­аль­ной тех­ни­ки, боль­шую часть с док­то­ром тех­ни­че­ских наук, про­фес­со­ром, ге­не­ра­лом Бла­го­нра­во­вым А.А. Спе­ци­а­лист в об­ла­сти ди­на­ми­ки и проч­но­сти машин, ме­ха­ни­че­ских транс­мис­сий, гид­ро­ме­ха­ни­че­ских и гид­ро­объ­ем­ных пе­ре­дач и в дру­гих об­ла­стях ма­ши­но­стро­е­ния.